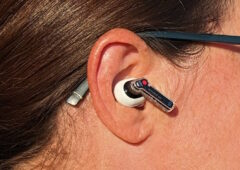
Test Nothing Ear : des écouteurs sans fil qui délivrent un son sur mesure
Les nouveaux écouteurs intra-auriculaires sans fil Ear de Nothing offrent des fonctions complètes pour un prix relativement raisonnable. Est-ce suffisant pour s’imposer comme l’un des meilleurs choix du moment ?